MySQL 底层存储 B-Tree 和 B+Tree 原理分析
为什么 MySQL 查询能快速找到数据?为什么索引能显著提升查询性能?答案就在于底层的索引结构——B+Tree。B+Tree 是 MySQL(特别是 InnoDB 引擎)最核心的数据结构,理解它的工作原理对于设计高性能数据库应用至关重要。本文将从基础概念出发,系统性地介绍 B-Tree 和 B+Tree 的原理、结构特点、操作复杂度以及在 MySQL 中的实际应用。
简介
什么是 B-Tree
B-Tree(Balanced Tree)是一种自平衡的多路搜索树,由 Rudolf Bayer 和 Ed McCreight 于 1972 年提出。B-Tree 中的 "B" 代表 "Balanced"(平衡),而不是 "Binary"(二叉)。
B-Tree 的设计目标是:最小化磁盘 I/O 次数。在数据库场景中,数据量大无法全部加载到内存,需要频繁进行磁盘读写,B-Tree 通过减少树的高度来降低磁盘访问次数。
什么是 B+Tree
B+Tree 是 B-Tree 的变体,也是目前数据库索引最常用的数据结构。MySQL 的 InnoDB 和 MyISAM 引擎都使用 B+Tree 作为索引结构。
B+Tree 相比 B-Tree 的主要改进:
- 所有数据记录都存储在叶子节点
- 非叶子节点只存储索引键值,不存储实际数据
- 叶子节点之间通过双向链表连接
为什么选择 B+Tree
| 数据结构 | 查找复杂度 | 磁盘 I/O | 适用场景 |
|---|---|---|---|
| 二叉树 | O(log n) | 较高 | 内存数据 |
| 红黑树 | O(log n) | 较高 | 内存数据 |
| 哈希表 | O(1) | 不支持范围查询 | 精确查找 |
| B-Tree | O(log n) | 低 | 文件系统 |
| B+Tree | O(log n) | 最低 | 数据库索引 |
MySQL 选择 B+Tree 的原因:
- 树的高度低:减少磁盘 I/O 次数
- 范围查询高效:叶子节点有序连接,适合范围扫描
- 节点利用率高:非叶子节点只存键值,能容纳更多索引项
- 查询性能稳定:所有查询都需要走到叶子节点
B-Tree 原理
B-Tree 的结构
B-Tree 是一棵多路平衡查找树,其结构特点如下:
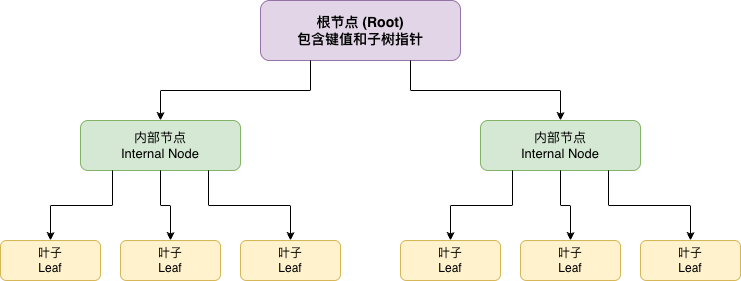
B-Tree 的性质
一棵 m 阶 B-Tree 必须满足以下性质:
节点键值数量限制
- 根节点:至少有 1 个键,最多有 2m - 1 个键
- 非根节点:至少有 m - 1 个键,最多有 2m - 1 个键
子树数量限制
- 每个节点最多有 2m 个子节点
- 每个非叶子节点(除根外)至少有 m 个子节点
键值有序
- 所有节点的键值按升序排列
- 每个节点的键值将子树分为若干区间
叶子节点在同一层
- 所有叶子节点都在同一层,树的高度平衡
键值与子树的关系
- 对于节点中的任意键值 K[i]:
- K[0] < K[1] < K[2] < ... < K[n-1]
- 子树 P[0] 中所有键 < K[0]
- 子树 P[i] 中所有键:K[i-1] < 键值 < K[i]
- 子树 P[n] 中所有键 > K[n-1]
- 对于节点中的任意键值 K[i]:
B-Tree 节点结构
1class BTreeNode:
2 def __init__(self, m: int, is_leaf: bool = False):
3 self.num_keys: int = 0 # 当前键值数量
4 self.is_leaf: bool = is_leaf # 是否为叶子节点
5 self.keys: List[int] = [0] * (2 * m - 1) # 键值数组
6 self.children: List['BTreeNode'] = [None] * (2 * m) # 子节点指针数组
B-Tree 查找操作
算法描述:
- 从根节点开始
- 在当前节点中二分查找目标键
- 如果找到,返回
- 如果没找到且当前节点不是叶子节点,根据键值大小选择合适的子节点继续查找
- 重复步骤 2-4,直到找到或到达叶子节点
时间复杂度: O(log n)
查找示例:
假设要查找键值 25:
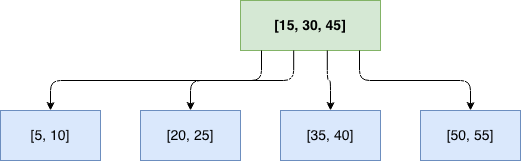
查找过程:
- 在根节点 [15, 30, 45] 中查找,25 > 15 且 25 < 30
- 转到第二个子节点 [20, 25]
- 在该节点中找到 25,查找成功
B-Tree 插入操作
插入算法:
- 查找插入位置,定位到叶子节点
- 如果叶子节点未满,直接插入
- 如果叶子节点已满(键值数达到 2m - 1):
- 将节点分裂为两个节点
- 中间键值上移到父节点
- 如果父节点也满,递归向上分裂
插入示例(m = 2):
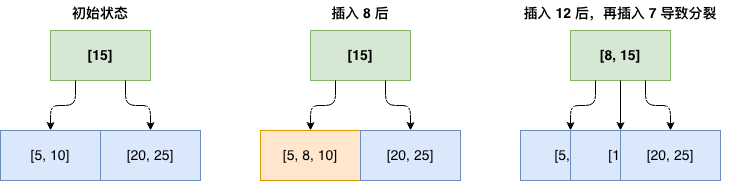
B-Tree 删除操作
删除算法:
- 查找要删除的键
- 情况1:在叶子节点删除
- 删除后节点键值数 >= m - 1,直接删除
- 删除后节点键值数 < m - 1(下溢):
- 从兄弟节点借一个键
- 兄弟节点也不足,合并节点
- 情况2:在内部节点删除
- 找到前驱或后继键替换
- 递归删除前驱或后继
删除示例:

B+Tree 原理
B+Tree 的结构
B+Tree 是 B-Tree 的改进版本,其结构特点如下:
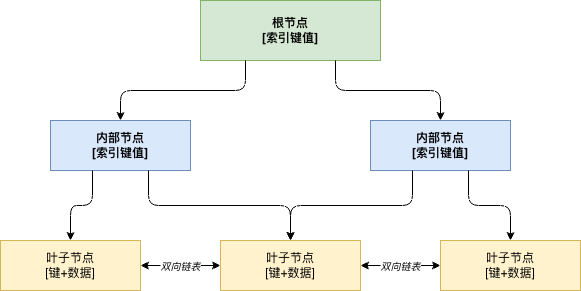
B+Tree 的性质
一棵 m 阶 B+Tree 必须满足以下性质:
节点键值数量限制
- 根节点:至少有 1 个键,最多有 m 个键
- 非根节点:至少有 ⌈m/2⌉ 个键,最多有 m 个键
子树数量限制
- 每个节点最多有 m 个子节点
- 每个非叶子节点(除根外)至少有 ⌈m/2⌉ 个子节点
数据存储位置
- 所有的数据记录都存储在叶子节点
- 非叶子节点只存储索引键值和子树指针
叶子节点连接
- 叶子节点之间通过双向链表连接
- 所有叶子节点按键值升序排列
键值重复
- 非叶子节点的键值会在子节点中重复出现
- 这是与 B-Tree 的重要区别
B+Tree 节点结构
1# 内部节点(非叶子节点)
2class BPlusTreeInternalNode:
3 def __init__(self, m: int):
4 self.num_keys: int = 0 # 键值数量
5 self.keys: List[int] = [0] * m # 键值数组
6 self.children: List[BPlusTreeNode] = [None] * (m + 1) # 子节点指针
7
8# 叶子节点
9class BPlusTreeLeafNode:
10 def __init__(self, m: int):
11 self.num_keys: int = 0 # 键值数量
12 self.keys: List[int] = [0] * m # 键值数组
13 self.data: List[Any] = [None] * m # 数据指针(指向实际数据)
14 self.prev: BPlusTreeLeafNode = None # 前驱节点指针
15 self.next: BPlusTreeLeafNode = None # 后继节点指针
B+Tree 查找操作
算法描述:
- 从根节点开始
- 在当前节点中查找目标键
- 如果当前节点是叶子节点,检查键是否存在
- 如果当前节点不是叶子节点,根据键值选择子节点继续查找
- 重复步骤 2-4,直到到达叶子节点
重要特点: 无论是否找到数据,都必须走到叶子节点,因为数据只存储在叶子节点中。
时间复杂度: O(log n)
B+Tree 插入操作
插入算法:
- 从根节点开始,找到合适的叶子节点
- 在叶子节点中插入键和数据
- 如果叶子节点满了(键值数达到 m):
- 将叶子节点分裂为两个
- 中间键值(分裂后的第一个键)上移到父节点
- 更新叶子节点的链表指针
- 如果父节点也满了,递归向上分裂
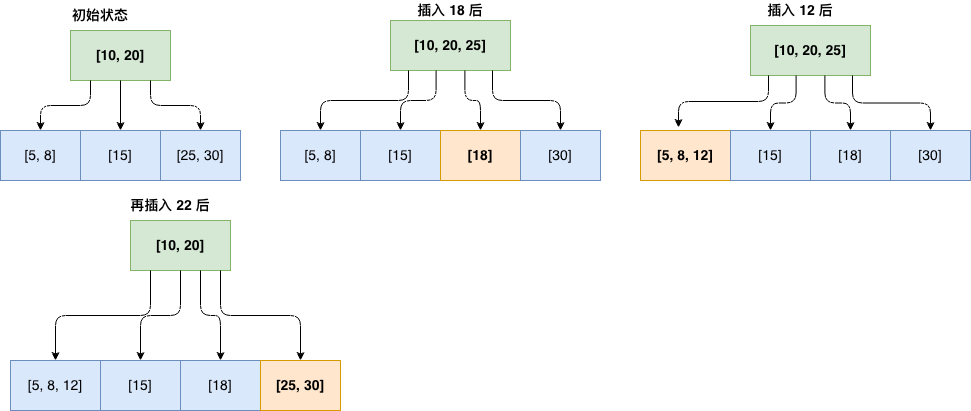
插入示例(m = 3):
B+Tree 删除操作
删除算法:
- 找到目标键所在的叶子节点
- 删除键和数据
- 检查叶子节点状态:
- 键值数 >= ⌈m/2⌉:删除完成
- 键值数 < ⌈m/2⌉(下溢):
- 尝试从兄弟节点借一个键
- 兄弟节点也不足,与兄弟节点合并
- 合并后可能导致父节点键值不足,递归处理
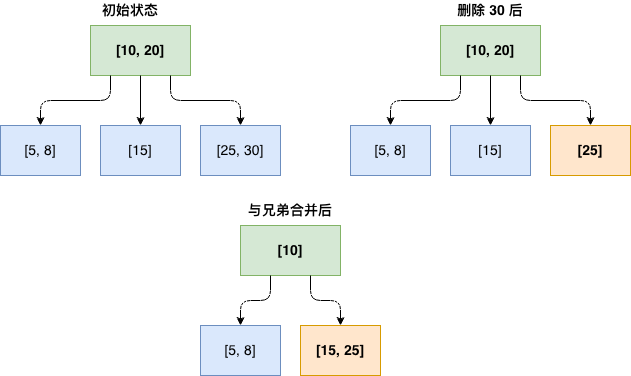
删除示例:
B-Tree vs B+Tree
结构对比
| 特性 | B-Tree | B+Tree |
|---|---|---|
| 数据存储 | 所有节点都可存储数据 | 数据只在叶子节点 |
| 非叶子节点 | 存储键和数据 | 只存储键 |
| 叶子节点 | 无特殊连接 | 双向链表连接 |
| 范围查询 | 需要中序遍历 | 直接遍历叶子链表 |
| 树的高度 | 相对较高 | 相对较低 |
性能对比
查询性能
| 场景 | B-Tree | B+Tree |
|---|---|---|
| 精确查询 | 可能更早找到 | 必须到叶子节点 |
| 范围查询 | 需要回溯 | 直接遍历链表 |
| 查询稳定性 | 不稳定 | 稳定 |
为什么 B+Tree 在数据库中表现更好?
- 磁盘 I/O 更少:非叶子节点不存数据,能容纳更多键,树更矮
- 范围查询高效:叶子节点有序连接,一次扫描即可
- 查询性能稳定:所有查询都走相同路径
示例:范围查询
查找键值在 [10, 30] 之间的数据:
B-Tree:
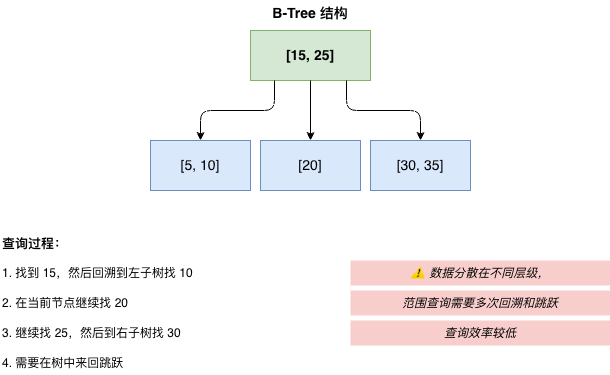
B+Tree:
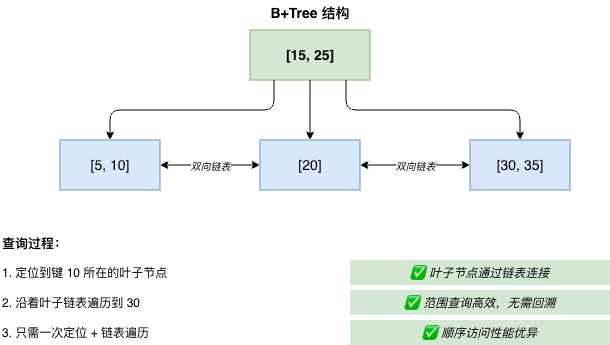
存储空间对比
假设每个节点能存储的键数量相同:
| 数据结构 | 非叶子节点 | 叶子节点 | 总数据量 |
|---|---|---|---|
| B-Tree | 键 + 数据 | 键 + 数据 | 相同 |
| B+Tree | 只存键 | 键 + 数据 | 相同 |
虽然存储的数据总量相同,但 B+Tree 的非叶子节点不存数据,能存储更多键,从而降低树的高度。
实际影响:
假设每页 16KB,每条记录 100 字节:
- B-Tree 非叶子节点:约 160 条(键+指针)
- B+Tree 非叶子节点:约 320 条(只有键+指针)
存储 1 亿条数据:
- B-Tree 高度:约 4-5 层
- B+Tree 高度:约 3-4 层
MySQL InnoDB 中的 B+Tree
InnoDB 索引结构
InnoDB 引擎使用 B+Tree 作为索引结构,分为两种类型:
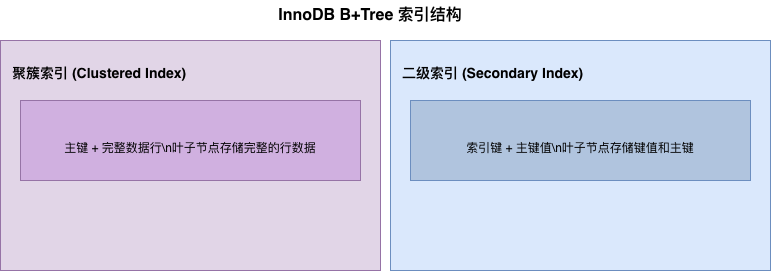
聚簇索引
定义: 聚簇索引是根据主键构建的 B+Tree,叶子节点存储完整的行数据。
特点:
- 每个表只能有一个聚簇索引
- 主键索引就是聚簇索引
- 数据文件本身就是索引文件
- 范围查询非常高效
查询示例:
1-- 使用聚簇索引查询
2SELECT * FROM user WHERE id = 100;
3
4-- 查询路径:根节点 → 内部节点 → 叶子节点(找到完整数据)
二级索引
定义: 二级索引是除主键索引外的其他索引,叶子节点存储索引键值和主键值。
特点:
- 一个表可以有多个二级索引
- 查询时需要先查二级索引,再通过主键回表
- 联合索引也是二级索引的一种
回表查询:
1-- 假设 name 有二级索引
2SELECT * FROM user WHERE name = 'Tom';
3
4-- 查询路径:
5-- 1. 在 name 的二级索引 B+Tree 中找到 'Tom'
6-- 2. 获取对应的主键 id = 100
7-- 3. 通过 id 在聚簇索引中查询完整数据(回表)
覆盖索引优化:
如果查询的列都包含在索引中,可以避免回表:
1-- 假设有联合索引 (name, age)
2SELECT name, age FROM user WHERE name = 'Tom';
3
4-- 无需回表,直接从二级索引获取数据
InnoDB B+Tree 参数
InnoDB 的 B+Tree 结构由以下参数控制:
| 参数 | 默认值 | 说明 |
|---|---|---|
innodb_page_size | 16KB | 数据页大小 |
innodb_buffer_pool_size | 128MB | 缓冲池大小 |
innodb_fill_factor | 100 | 页填充因子 |
页面大小的影响:
1-- 查看页面大小
2SHOW VARIABLES LIKE 'innodb_page_size';
- 页面越大:每页能存储更多索引项,树的高度更低
- 页面越小:并发写入冲突更少,但树的高度更高
InnoDB B+Tree 实际结构
1-- 创建测试表
2CREATE TABLE user (
3 id INT PRIMARY KEY,
4 name VARCHAR(50),
5 age INT,
6 email VARCHAR(100)
7);
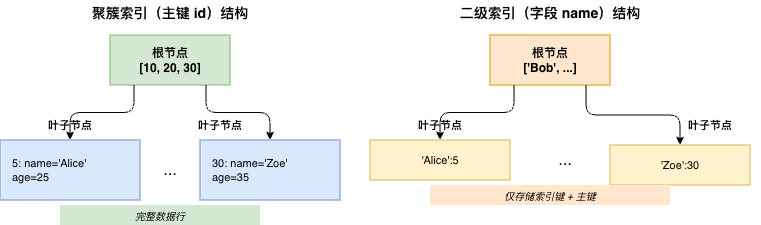
B+Tree 的应用场景
1. 主键索引
1-- 最常见的应用
2CREATE TABLE orders (
3 id BIGINT PRIMARY KEY,
4 order_no VARCHAR(32),
5 user_id BIGINT,
6 amount DECIMAL(10,2),
7 created_at TIMESTAMP
8);
9
10-- 查询利用聚簇索引
11SELECT * FROM orders WHERE id = 123456;
2. 二级索引
1-- 为常用查询条件创建索引
2CREATE INDEX idx_user_id ON orders(user_id);
3CREATE INDEX idx_created_at ON orders(created_at);
4
5-- 联合索引(最左前缀原则)
6CREATE INDEX idx_user_created ON orders(user_id, created_at);
3. 联合索引
联合索引的 B+Tree 按照索引定义的顺序组织:
1-- 联合索引 (user_id, created_at)
2CREATE INDEX idx_user_created ON orders(user_id, created_at);
3
4-- ✅ 可以使用索引
5SELECT * FROM orders WHERE user_id = 100;
6SELECT * FROM orders WHERE user_id = 100 AND created_at > '2024-01-01';
7
8-- ❌ 不能使用索引(违反最左前缀)
9SELECT * FROM orders WHERE created_at > '2024-01-01';
联合索引结构:
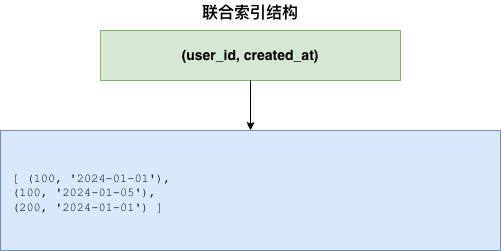
4. 前缀索引
对于长字符串字段,可以使用前缀索引节省空间:
1-- 对 email 创建前缀索引
2CREATE INDEX idx_email_prefix ON orders(email(20));
3
4-- 对备注字段创建前缀索引
5CREATE INDEX idx_comment_prefix ON article(comment(100));
注意: 前缀索引无法用于覆盖索引和排序。
性能优化
1. 选择合适的索引
1-- ✅ 好的索引:高频查询条件
2CREATE INDEX idx_user_status ON user(user_id, status);
3
4-- ❌ 不好的索引:低区分度的字段
5CREATE INDEX idx_gender ON user(gender); -- gender 只有男/女,区分度低
6
7-- ❌ 冗余索引
8CREATE INDEX idx_a ON table(a);
9CREATE INDEX idx_a_b ON table(a, b); -- idx_a 可以被 idx_a_b 覆盖
2. 利用覆盖索引
1-- 假设有联合索引 (user_id, status, created_at)
2
3-- ✅ 覆盖索引,无需回表
4SELECT user_id, status, created_at
5FROM orders
6WHERE user_id = 100;
7
8-- ❌ 需要回表
9SELECT * FROM orders WHERE user_id = 100;
3. 避免索引失效
1-- ✅ 可以使用索引
2SELECT * FROM orders WHERE user_id = 100;
3SELECT * FROM orders WHERE user_id > 100;
4
5-- ❌ 索引失效:对字段进行函数运算
6SELECT * FROM orders WHERE UPPER(user_name) = 'TOM';
7
8-- ❌ 索引失效:类型转换
9SELECT * FROM orders WHERE user_id = '100'; -- 字符串转数字
10
11-- ✅ 解决方案:使用函数索引或正确类型
12SELECT * FROM orders WHERE user_id = 100;
4. 索引优化技巧
避免在索引列上使用运算:
1-- ❌ 索引失效
2SELECT * FROM orders WHERE user_id + 1 = 101;
3
4-- ✅ 优化后
5SELECT * FROM orders WHERE user_id = 100;
使用正确的比较运算符:
1-- ✅ 使用索引
2WHERE user_id IN (1, 2, 3)
3
4-- ❌ 可能不使用索引(取决于优化器)
5WHERE user_id NOT IN (1, 2, 3)
常见问题
Q1: 为什么不用 Hash 索引?
Hash 索引只支持精确查找,不支持范围查询:
1-- ✅ Hash 索引支持
2SELECT * FROM user WHERE id = 100;
3
4-- ❌ Hash 索引不支持
5SELECT * FROM user WHERE id BETWEEN 100 AND 200;
6SELECT * FROM user WHERE id > 100;
7SELECT * FROM user ORDER BY id;
Q2: 为什么不用二叉树?
二叉树的问题:
- 树的高度高:n 个数据需要 log₂n 层
- 每层访问一次磁盘:磁盘 I/O 次数多
- 缓存局部性差:节点分散在磁盘不同位置
对比:
| 数据结构 | 1亿条数据的高度 |
|---|---|
| 二叉树 | 约 27 层 |
| B+Tree | 约 3-4 层 |
Q3: 主键选择对性能的影响
1-- ❌ 不好的主键:长字符串
2CREATE TABLE order_log (
3 order_no VARCHAR(32) PRIMARY KEY, -- 主键太长,B+Tree 深度高
4 content TEXT
5);
6
7-- ✅ 好的主键:自增整数
8CREATE TABLE order_log (
9 id BIGINT AUTO_INCREMENT PRIMARY KEY,
10 order_no VARCHAR(32),
11 content TEXT
12);
主键选择原则:
- 长度小:减少 B+Tree 深度
- 自增:减少页分裂
- 稳定:避免频繁更新
Q4: 如何查看索引使用情况?
1-- 查看表的索引
2SHOW INDEX FROM user;
3
4-- 使用 EXPLAIN 分析查询执行计划
5EXPLAIN SELECT * FROM user WHERE id = 100;
6
7-- 查看索引使用统计(MySQL 8.0+)
8SELECT * FROM performance_schema.table_io_waits_summary_by_index_usage
9WHERE OBJECT_SCHEMA = 'your_database';
Q5: 什么情况下索引会失效?
| 场景 | 索引是否使用 |
|---|---|
WHERE id = 1 | ✅ 使用 |
WHERE id + 1 = 2 | ❌ 失效 |
WHERE UPPER(name) = 'A' | ❌ 失效 |
WHERE name LIKE 'A%' | ✅ 使用(前缀匹配) |
WHERE name LIKE '%A' | ❌ 失效(后缀匹配) |
WHERE name LIKE '%A%' | ❌ 失效(全匹配) |
WHERE id IS NULL | ✅ 使用 |
WHERE id IN (1, 2) | ✅ 使用 |
ORDER BY id | ✅ 使用 |
总结
B+Tree 是 MySQL 数据库索引的核心数据结构,理解它的工作原理对于数据库性能优化至关重要。
核心要点:
B-Tree 特点:
- 多路平衡查找树
- 所有节点都可存储数据
- 非叶子节点既有键也有数据
B+Tree 特点:
- 数据只在叶子节点
- 叶子节点通过双向链表连接
- 非叶子节点只存键
- 范围查询高效
MySQL InnoDB 索引:
- 聚簇索引:主键索引,叶子节点存储完整行数据
- 二级索引:非主键索引,叶子节点存储键和主键
- 查询时可能需要回表
优化建议:
- 合理选择索引字段,避免冗余
- 利用覆盖索引减少回表
- 避免在索引列上进行函数运算
- 选择合适的主键类型和长度
- 定期分析索引使用情况,删除无用索引
理解 B+Tree 的工作原理,可以帮助我们更好地设计数据库结构,优化查询性能,构建高效的应用系统。